Estudio de las Cónicas:

Las cónicas constituyen uno de los conjuntos de curvas más importantes de la Geometría y que más se utilizan en distintas ramas de la Ciencia y la Ingeniería. 

Tradicionalmente, el estudio de las cónicas en el bachillerato es un estudio de tipo analítico, destinado a obtener sus ecuaciones en un determinado sistema de referencia, partiendo de unas definiciones que, en algunos casos, parecen sacadas de una chistera y deducir de ellas sus propiedades. Este enfoque práctico, no permite vislumbrar la belleza que esconden estas curvas al estudiar sus propiedades por métodos puramente geométricos; de hecho, ni siquiera sirve para justificar el nombre de cónicas ni permite saber de dónde han salido esas definiciones.

En este trabajo se hace una presentación de las cónicas desde un punto de vista totalmente geométrico. Se muestran cada una de estas curvas como intersección de un plano con un cono de revolución y, posteriormente, se demuestran sus propiedades utilizando las demostraciones basadas en las esferas de Dandelin.

Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Se clasifican en tres tipos: elipses, parábolas e hipérbolas.

Información de las cónicas, su construcción, historia, applets animados realizados con el programa regla y compas 

La Parábola

La Hipérbola

La Elipse

La Parábola

Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.

La distancia entre el foco y la directriz de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p). Dada una parábola, se llama eje de la misma la recta que contiene al foco y es perpendicular a la directriz. Se llama vértice de la parábola al punto donde ésta corta a su eje.

La ecuación para una parábola con eje focal paralelo al eje x, vértice en (h, k) y cuya distancia al foco es p es:

La ecuación para una parábola con eje focal paralelo al eje y,  vértice en (h, k) y cuya distancia al foco es p es:

Construcción

Se debe tomar una hoja de acetato en ella se dibuja un punto. Para construir la parábola se dobla la hoja de tal manera que cualquier punto del borde inferior coincida con el punto dibujado y desdoblamos la hoja. Haciendo este procedimiento varias veces con un punto distinto del borde inferior cada vez, tendremos que las marcas de los dobleces han formado una parábola. El punto dibujado es el foco y el borde inferior de la hoja, la directriz.

Otra forma de encontrar una parábola es la siguiente. Se debe hacer un corte a un cono de unicel con un plano, la dirección del corte debe ser desde la base del cono a cualquier punto del cono. El perímetro de este corte será una parábola.

-Aplicaciones

Las aplicaciones de las parábolas son básicamente aquellos fenómenos en donde nos interesa hacer converger o divergir un haz de luz y sonido principalmente. Por ejemplo las atenas parabólicas, las lámparas sordas, los faros de los autos. Se pueden construir, por la misma propiedad de las parábolas, hornos solares. Los micrófonos de ambiente en algunos deportes también tienen forma paraboloidal.

Las parábolas tienen una propiedad  Si se coloca una bombilla encendida en el foco de la parábola, algunos haces de luz serán reflejados por la parábola y todos estos rayos serán perpendiculares a la directriz. Esta propiedad es usada en las lámparas sordas o en los faros de los automóviles estos están formados por un paraboloide (parábola en 3 dimensiones) de espejos y una bombilla en el foco de este paraboloide. En algunas lámparas se puede mover la bombilla del foco y los haces de luz divergieran o convergerán. Este principio funciona también en las antenas parabólicas. Un satélite envía información a la Tierra, estos rayos serán perpendiculares a la directriz por la distancia a la que se encuentra el satélite. Al reflejarse en el plato de la antena (blanca, casi siempre) los rayos convergen en el foco en donde se encuentra un receptor que decodifica la información. También en los telescopios se usa esta propiedad.

Ejemplo:  Determinar, en forma reducida, las ecuaciones de las siguientes parábolas, indicando el valor del parámetro, las coordenadas del foco y la ecuación de la directriz.

1 

2 

La Hipérbola

Se llama hipérbola al lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es una constante (se representa por 2a).

La recta que une los dos focos se llama eje real de la hipérbola y la mediatriz se llama eje imaginario de la hipérbola. El punto donde se cortan ambos ejes (que es el punto medio de los focos) se llama centro de la hipérbola. Los puntos donde la hipérbola corta a los ejes se llaman vértices de la hipérbola. Al igual que en la elipse, se llama distancia focal a la distancia entre los dos focos y a las distancias desde un punto cualquiera de la hipérbola a ambos focos se les llama radios vectores del punto

-Construcción

Se debe tomar una hoja de acetato, en ella se dibuja una circunferencia y un punto fuera de ella. Para construir una hipérbola se dobla la hoja de tal manera que cualquier punto de la circunferencia coincida con el punto dibujado y desdoblamos la hoja. Haciendo este procedimiento varias veces con un punto distinto de la circunferencia cada vez, tendremos que las marcas de los dobleces han formado una hipérbola. El punto dibujado es un foco y el centro de la circunferencia es el otro foco.

Otra forma de encontrar una hipérbola es la siguiente. Se colocan dos conos unidos en su vértice y se hace un corte de base a base de los conos. El perímetro de este corte será una elipse.

-Aplicaciones

La Hipérbola tiene propiedades de reflexión análogas a las de la elipse. Si se dirige un haz de luz en dirección de un foco, por ejemplo de f, se reflejará antes de llegar a él en la hipérbola en dirección del foco f'. Este principio se usa en los telescopios del tipo Cassegrain. El sistema de navegación loran (acrónimo de long range navigation) usa las propiedades de la reflexión de la hipérbola

Las hipérbolas aparecen en muchas situaciones reales, por ejemplo, un avión que vuela a velocidad supersónica paralelamente a la superficie de la tierra, deja una huella acústica hiperbólica sobre la superficie. La intersección de una pared y el cono de luz que emana de una lámpara de mesa con pantalla troncocónica, es una hipérbola.

La definición de la hipérbola como lugar geométrico es similar a la dada para la elipse, como vemos en seguida

La recta que pasa por los focos corta a la hipérbola en dos puntos llamados vértices. El segmento recto que une los vértices se llama eje transversal y su punto medio es el centro de la hipérbola. Un hecho distintivo de la hipérbola es que su gráfica tiene dos partes separadas, llamadas ramas.

Figura 1.

 

  Los vértices están a una distancia de a unidades del centro y los focos a una distancia de unidades del centro. Además

Figura 2.

  Resumiendo:

Si el eje transversal de la hipérbola es horizontal entonces

• El centro está en

• Los vértices están en 

• Los focos están en

Si el eje transversal de la hipérbola es vertical entonces

• El centro está en 

• Los vértices están en 

• Los focos están en 

Una ayuda importante para trazar la gráfica de una hipérbola son sus asíntotas. Toda hipérbola tiene dos asíntotas que se intersecan en su centro y pasan por los vértices de un rectángulo de dimensiones 2a  y 2b  y centro en 

El segmento recto de longitud 2b  que une

se llama eje conjugado de la hipérbola. El siguiente teorema identifica la ecuación de las asíntotas.

Observación: las asíntotas de la hipérbola coinciden con las diagonales del rectángulo de dimensiones  y  centro

Esto sugiere una forma simple de trazar tales asíntotas.

Si la excentricidad es grande los focos están cerca del centro y las ramas de la hipérbola son casi rectas verticales. Si la excentricidad es cercana a uno los focos están lejos del centro y las ramas de la hipérbola son más puntiagudas.

La propiedad reflectora de la hipérbola afirma que un rayo de luz dirigido a uno de los focos de una hipérbola se refleja hacia el otro foco (figura 2).

Figura 3.

Ejemplo 1

Hallar la ecuación canónica, los focos, los vértices, la excentricidad y las asíntotas de la hipérbola cuya ecuación es

Solución

Completando el cuadrado en ambas variables

La gráfica se muestra en la figura 3.

Figura 4.

Ejemplo 2

Por tanto, la ecuación canónica es

El valor de está dado por

Figura 5.

La Elipse

Se llama elipse al lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos, llamados focos, es una constante. La línea que une los dos focos se llama eje principal de la elipse y la mediatriz de los mismos eje secundario. Se llaman vértices de la elipse a los puntos donde ésta corta a sus ejes. El punto medio de los dos focos se llama centro de la elipse y la distancia entre ellos se llama distancia focal.

-Construcción

Se debe tomar una hoja de acetato, en ella se dibuja una circunferencia y un punto dentro de ella.

 Para construir una elipse se dobla la hoja de tal manera que cualquier punto de la circunferencia coincida con el punto dibujado y desdoblamos la hoja.

Haciendo este procedimiento varias veces con un punto distinto de la circunferencia cada vez, tendremos que las marcas de los dobleces han formado una elipse. El punto dibujado es un foco y el centro de la circunferencia es el otro foco.

Otra forma de encontrar una elipse es la siguiente. Se debe hacer un corte a un cono de unicel con un plano, la dirección del corte debe ser de lado a lado de las paredes del cono sin llegar a la base. Mientras mas paralelo a la base sea el corte menos excentricidad tendrá la elipse. El perímetro de este corte será una elipse

-Aplicaciones

La elipse tiene propiedades de reflexión similares a la de la parábola, en este caso cuando colocamos un emisor de ondas en un foco, estas se reflejarán en las paredes de la elipse y convergerán en el otro foco. Con respecto a la elipse la aplicación primera que tenemos que mencionar es que las órbitas de los planetas son elípticas con el Sol en uno de los focos.

En la medicina se usa un aparato llamado litotriptor para desintegrar "cálculos" renales por medio de ondas intra-acuáticas de choque. El funcionamiento de este aparato es de la siguiente forma, se coloca un medio elipsoide lleno de agua pegado al cuerpo del paciente en el foco de esta parte del elipsoide se pone un generador de ondas; el foco de la otra parte del elipsoide se debe localizar en estos "cálculos" y así al reflejarse las ondas en la superficie de la elipsoide de afuera del paciente todas convergerán en el "cálculo" y este se desintegrará. Además existen capillas o galerías de los secretos. Son estructuras con techos elipsoidales aquí se puede oír a una persona que está en un foco desde el otro foco y las personas que están entre las otras dos no oirá nada.

Más de mil años después de que los griegos definieran las secciones cónicas, en la época del Renacimiento, el astrónomo polaco Nicholas Copérnico (1473 - 1543), en su obra: Sobre las revoluciones de las esferas celestes, sostenía que todos los planetas, incluso la Tierra, giraban en órbitas circulares alrededor del Sol. Aunque muchas de las afirmaciones de Copérnico no eran válidas la controversia provocada por su teoría heliocéntrica empujó a los astrónomos a buscar un modelo matemático que explicará los movimientos de los planetas y el Sol. El primero en hallarlo fue el astrónomo alemán Johannes Kepler (1571 - 1630).Kepler descubrió que los planetas giran alrededor del Sol en órbitas elípticas, con el Sol colocado no en el centro sino en uno de los focos. El uso de las elipses para explicar el movimiento de los planetas es tan sólo una de sus diversas aplicaciones. Al igual que lo hicimos para la parábola vamos a definir la elipse como un lugar geométrico de puntos. En este caso usando dos puntos focales en vez de uno.

La recta que pasa por los focos corta a la elipse en dos puntos llamados vértices. La cuerda que une los vértices es el eje mayor de la elipse y su punto medio el centro de la elipse. La cuerda perpendicular al eje mayor y que pasa por el centro se llama eje menor de la elipse.

Para visualizar la definición de la elipse, basta imaginar dos chinches clavados en los focos y un trozo de cuerda atada a ellos. Al ir moviendo un lápiz que tensa esa cuerda, su trazo irá dibujando una elipse, como se muestra en la figura 1.

Figura 1.

  En el programa que sigue, el primer segmento determina la constante 2a. Esta constante se puede modificar arrastrando ambos puntos del segmento. Los focos también se pueden modificar arrastrándolos con el mouse. El punto sobre la línea azul sirve para variar la pendiente de la recta

 

  

Figura 2.

Observación: de la figura 2, podemos deducir que

es decir, es la constante a la que se refiere la definición.

Los focos están en el eje mayor a unidades del centro con

y el eje mayor es horizontal. En el caso de que el eje mayor sea vertical la ecuación toma la forma:

Observación: la demostración de este teorema no es complicada, basta aplicar la definición y la fórmula de distancia (figura 2).

Simplificando

Pero,

y así obtenemos la ecuación canónica de la elipse

La excentricidad es una medida de la "circularidad" de una elipse, entre más cerca de cero más circular y entre más cerca de uno más alargada.

Observe que al estar situados los focos en el eje mayor entre el centro y los vértices, siempre se tiene que

Es decir, las elipses tienen una excentricidad menor a uno.

Esto explica la dificultad de los astrónomos en detectar las órbitas elípticas de los planetas, pues estas tienen los focos muy cerca de su centro, lo cual las hace casi circulares. La siguiente tabla muestra la excentricidad de las órbitas de los nueve planetas y la Luna.

Una de las propiedades geométricas más interesante de la elipse afirma que: un rayo que emana de uno de los focos de la elipse y se refleja en ella pasa por el otro foco; esta propiedad se conoce como la propiedad reflectora (figura 3).

 

Figura 3.

Ejemplo 1

Hallar la ecuación canónica de la elipse

Trazar su gráfica identificando los vértices, los focos, el centro y la excentricidad.

Solución

Para hallar la ecuación canónica debemos completar el cuadrado de la expresión en ambas variables e

La gráfica se muestra en la figura 4.

Figura 4.

Ejemplo 2

La gráfica de la elipse se muestra en la figura 5.

Figura 5.

Leyes de Kepler 

1ra ley de Kepler: Las Orbitas son Elípticas 

Con las observaciones de Tycho Brahe, Kepler se decidió en determinar si las trayectorias de los planetas se podrían describir con una curva. Por ensayo y error, descubrió que una elipse con el Sun en un foco podría describir acertadamente la órbita de un planeta sobre el Sol.

Fundamentalmente, las elipses son descritas por la longitud de sus dos ejes. Un círculo tiene el mismo diámetro si se le mide a lo ancho, hacia arriba y hacia abajo. Pero una elipse tiene diámetros de diversas longitudes. El más largo se llama el eje mayor, y el más corto es el eje menor. El radio de estas dos longitudes determina la excentricidad (e) de la elipse; mide cuán elíptica es. Los círculos tienen e=0, y las elipses muy estiradas hacia fuera tienen una excentricidad casi igual a 1.

Los planetas se mueven en elipses, pero son casi circulares. Los cometas son un buen ejemplo de objetos en nuestro Sistema Solar que pueden tener órbitas muy elípticas. Compare las excentricidades y las órbitas de los objetos que aparecen en en el diagrama.

Una vez que kepler determino que los planetas se mueven al rededor del sol en elipses, entonces descubrió otro hecho interesante sobre las velocidades de planetas a medida que circundan el Sol.

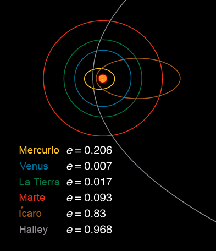
Diagrama que muestra las órbitas elípticas de algunos objectos del sistema solar. 

Los planetas describen órbitas elípticas estando el Sol en uno de sus focos

r₁ es la distancia más cercana al foco (cuando q=0) y r₂ es la distancia más alejada del foco (cuando q=p).

Una elipse es una figura geométrica que tiene las siguientes características:

• Semieje mayor a=(r₂+r₁)/2

• Semieje menor b

• Semidistancia focal c=(r₂-r₁)/2

• La relación entre los semiejes es a²=b²+c²

• La excentricidad se define como el cociente e=c/a=(r₂-r₁)/(r₂+r₁)

2da ley de Kepler: La velocidad de los planetas. 

Kepler descubrió su segunda ley por ensayo y error. Kepler se dió cuenta de que la línea que conecta a los planetas y al Sol abarca igual área en igual lapso de tiempo. Mire el diagrama que aparece a la izquierda. Lo que Kepler encontró es que lleva la misma cantidad de tiempo para el planeta azul vaya de A a B mientras al igual que para ir de C a D. Pero la distancia de C a D es mucho más grande que la de A a B. Tiene que ser de modo que las regiones verdes tengan la misma área. De manera que el planeta debe moverse más rápidamente entre C y D que entre A y B. Esto significa que cuando los planetas están cerca del Sol en su órbita, se mueven más rápidamente que cuando están más lejos.

La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular ${\displaystyle L}$es el producto de la masa del planeta, su velocidad y su distancia al centro del Sol.

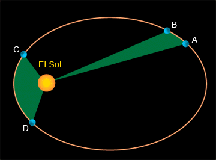
Diagrama que muestra el recorrido de un planeta alrededor del Sol.

El trabajo de Kepler lo llevó a un importante descubrimiento sobre las distancias de planetas.

 3ra Ley de Kepler: ley de Kepler: P² = a³

La 3^ra. ley de Kepler es una fórmula matemática. Significa que si usted sabe cuánto tiempo toma un planeta en circundar el Sol (p), después usted puede determinar a cuál distancia s e encuentra el planeta del Sol (a = eje semimayor de la órbita del planeta).

Esta fórmula también nos dice que los planetas lejanos del Sol tardan más tiempo en circundar al Sol que los que se encuentran cercanos al Sol. Se mueven más lentamente alrededor del Sol.

No dejes de ver la tabla de datos originales de los planetas . 

Notarás que el período orbital de los planetas (P) se hace más de largo a medida que va de Mercurio a Plutón. 

   

                                                    

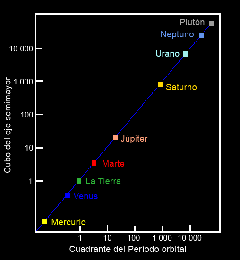
Un gráfico que muestra las tercera Ley de Kepler.